개요
3차원 그래픽에서 사실같은 렌더링을 할때 꼭 필요한 요소는 바로 조명이다.
지금까지는 정점 별 색상을 이용해 물체의 특정 픽셀의 색상을 정했다. 하지만 이제부터는 광원과 해당 물체의 표면점의 위치와 면한 방향, 재질, 시점의 위치 등를 이용해서 해당 빛을 표면점이 반사해서 시점에 들어오며 나타나게될 색상을 정할 것이다.
법선 벡터
법선 벡터는 물체의 표면점이 면한 방향을 나타내는 벡터이다. 좀 더 수학적으로는 해당 점의 접 평면에 수직인 벡터이다.(앞면 방향)
조명 렌더링을 위해선 각 표면점의 법선벡터가 필요한데 모든 점에 법선벡터를 일일히 설정할 수 없으므로 그 표면점의 삼각형을 나타내는 정점들에 정점 법선을 부여한다. 이후 래스터화 과정에서 해당 표면점에 해당하는 픽셀의 법선 벡터를 삼각형의 세정점의 정점법선을 삼각 보간하여 구한다. 이때 그러한 정점들의 정점법선을 구하는방법은 크게 다음 두가지로 나눠진다.
평평한 삼각형
평평한 삼각형을 만드려면 각 정점이 해당 삼각형의 면법선을 법선 벡터로 가지면된다. 그러면 그 삼각형의 표면점은 같은 세 벡터의 삼각보간을 통해 면법선을 그대로 가지게 된다. 이때 box등의 기하구조에서 한 점이 여러 다른 방향의 삼각형에 포함 될 수 있기에 위치는 같지만 법선벡터는 다른 각각의 정점으로 표현 되어야한다. box같은 경우 기존에는 8개의 정점으로 표현됬지만 지금은 한 사각형 면당 4개의 정점(그 면의 법선벡터를 가지는)으로 구현되어야하므로 8x6=24개의 정점으로 표현되어야 한다. 그러한 정점들과 그에 맞는 색인으로 평평한 법선들을 가지는 box메쉬를 표현할 수 있다.
둥근면 삼각형
구나 원기둥, 산악지형등의 메쉬들은 삼각형들의 모음으로 둥근면을 근사한다. 이때 이러한 삼각형 면들의 표면점에는 삼각형의 면법선이 아닌 우리가 근사하고자하는 둥근 면의 표면점의 법선을 부여하면 실제 둥근면처럼 느껴지는 조명효과를 줄 수 있다. 이러한 법선을 표면점들에 부여하려면 삼각형의 각 정점들의 정점 법선에 면법선이 아닌 해당 정점부분이 근사하고자하는 둥근 구조에서의 법선을 가지게 하면 된다. 이러한 법선을 근사 방법은 대표적으로 두가지가 있는데 하나는 정점 법선 평균 기법이 있고 다른 하나는 평면방정식의 편미분을 통한 접벡터 두개를 구해 외적하는 방법이 있다. 정점 법선 평균 기법은 해다 정점이 속한 삼각형들의 면법선을 모두 더한뒤 정규화시켜 정점 법선을 구한다. 다시 말해 색인버퍼에서 각 삼각형들을 가져와서 면법선을 구한뒤 그 삼각형을 만드는 정점들의 법선 벡터에 면법선을 모두 더해준다. 모든 삼각형의 면법선들을 더했다면 각 정점들의 법선벡터를 모두 정규화시켜주면 정점법선들이 완성된다. 후자의 경우는 해당 도형에 대한 미분가능 방정식이 주어진다면 사용할 수 있다.
정점 위치와 마찬가지로 정점법선 역시 일단 로컬 기준으로 생성해둔다. 이후 렌더아이템을 렌더링 할 때 그 아이템의 월드행렬을 위치와 정점법선에 적용하며 렌더링 된다. 정점 법선의 경우 방향을 나타내는 벡터이기에 위치이동은 적용되지 않지만 회전변환이나 비례변환같은 경우에는 벡터에 변환이 있을 수 있다. 이때 비균등 비례변환의 경우 위치에 적용되는 변환 행렬을 그대로 적용시키면 왜곡이 일어난다. 따라서 비균등 비례변환은 변환행렬의 역전치행렬을 곱해주어야한다. 이때 회전변환의 경우 전치행렬이 곧 역행렬이므로 역전치를 해도 그대로 유지된다. 따라서 법선벡터에는 변환행렬의 역전치행렬을 곱해주면 비균등비례변환을 포함한 변환도 정상적으로 적용된다. 비균등비례변환이 없다는게 보장된다면 변환행렬을 그대로 곱해주어도 상관없다.
조명 주요 벡터들
다음은 조명 렌더링에 쓰이는 주요 벡터들이다.
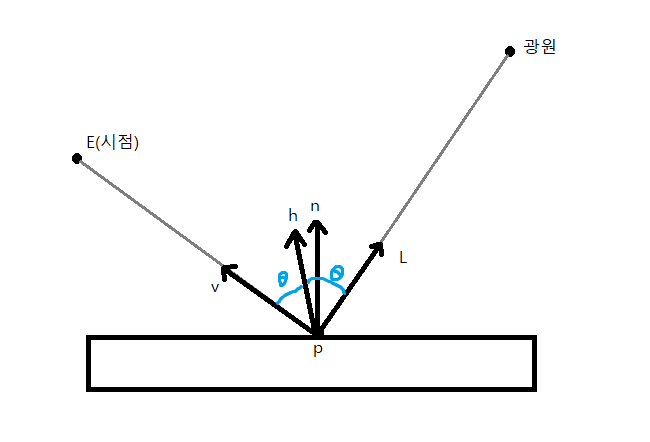
해당 벡터들은 모두 단위벡터이다.
p: 표면점
n: 표면점의 법선벡터
L: 표면에서 광원을 가르키는 벡터
v: 표면에서 시점을 가르키는 벡터
h: 광원의 빛이 반영반사되었을 때 v방향으로 반산되도록하는 법선벡터(거칠기에 의한 미시법선을 나타낸다.)
추가로 그림에는 없지만 실제 광원에서의 빛이 표면점에서 n법선벡터에 의해 반영반사된 방향의 벡터를 반사벡터(r)이라고 한다. 이 벡터는 우리가 사용할 계산에 조명 직접 사용되지는 않지만 해당 계산을 설명 및 유도하는 과정에서 자주 사용된다.
조명 렌더링
이제 본격적으로 조명을 이용한 픽셀 렌더링을 해보자.
우리가 사용할 근사 조명 방정식에서는 어떤 한 광원에서 출발하여 표면점에서 반사되어 시점에 들어오게되는 빛에는 다음 세가지가 있다.
1. 분산 반사광: 표면에서 모든 방향에 분산 반사되는 반사광이다. 재질의 분산반사율로 표면의 기본적인 색상을 나타낸다.
2. 반영 반사광: 빛이 법선에 의해 한 각도로 반사되어 시점에도 영향을 받으며 빛나는 반사광이다. 재질의 거칠기, 프레넬계수등으로 반짝임 매끄러움등의 특성을 나타난다.
3.주변 반사광: 현실에서는 광원에 의한 직접적인 빛뿐 아니라 다른 요소들에서 반사되어온 수많은 빛들이 표면점에 들어오게된다. 이러한 모든 빛을 계산할 수는 없기에 단순 상수로 이러한 주변광을 근사하고 분산반사율로 반사된 주변반사광을 계산한다. 주변광 상수의 설정으로 장면의 전체적인 분위기를 나타낼 수 있다.
람베르트 코사인 법칙
위 세가지 반사광을 공부하기 전 빛의 기본적인 법칙을 이야기하겠다.
빛이 한 표면점을 때릴 때 이를 미시적 관점으로 보면 수많은 광자들이 해당 표면점의 미시표면을 때리는 것으로 볼 수 있다. 이때 일정한 간격의 광자들이 미시표면을 때릴 때 광선 방향이 표면에 수직일 수 록 때리는 미시표면이 좁아 질 것이고 비스듬 할 수록 넓은 미시표면을 때릴 것이다. 이때 표면에 전달되는 빛의 밀도는 표면점의 법선벡터와 빛벡터L사이의 각도의 코사인에 비례한다. 즉 n과 L의 내적에 비례한다. 따라서 빛이 수직으로 표면점을 때릴때의 빛의 세기를 E1이라고 할때 각도a로 비스듬하게 표면점을 때리는 빛은 E1 * n⋅L의 세기를 가진다. 이러한 법칙을 람베르트 코사인 법칙이라고한다.
이때 cos(a)는, 즉 n⋅L은 표면의 뒷면으로 빛이 들어올 때 음수값이 나오게되는데 원래 뒷면으로 들어온 빛은 표면에 전혀 도달하지 않았다는 의미로 0의 값이 나오도록하는것이 맞다. 따라서 E1 * max(n⋅L,0)의 계산식으로 입사광의 세기를 계산하면 앞면은 법칙에 의한 적절한 값이, 뒷면은 0의 값을 가지게 되므로 이를 사용한다.
이러한 법칙은 분산 반사광과 반영 반사광을 구할 때 기본 빛의 세기에서 빛이 들어간 각도에 대해 한번 세기를 감쇠하고 계산하는데 사용된다. 주변반사광은 모든방향에서 동일하게 빛이 들어온다고 가정하므로 이를 사용하지 않는다.
분산 반사광
분산 반사는 물체의 표면에 도달한 빛이 표면에 살짝 들어갔어가 이리저리 반사하다 일부는 흡수되고 일부는 표면위의 180도 방향으로 동일하게 퍼져나가는 반사를 나타낸다. 물론 현실에서 모든 방향으로 동일하게 흩어지지는 않지만 우리가 사용할 근사 방정식에서는 동일하다고 가정한다. 분산반사는 해당 표면의 재질이 빛을 흡수한 뒤 반사하는 rgb의 비율을 나타내는 분산반사율이라는 재질특성에 의해 계산될 수 있다.
앞의 람베르트 코사인 법칙과 결합하여 표면점에 들어온 빛은 시점 위치에 상관없이 다음의 빛을 시점으로 반사한다. 빛의 기본 세기는 E, 분산반사율은 m이라고 하자
분산 반사광 = ( max(n⋅L,0) * E ) ⓧ m
반영 반사광
표면에 도달한 빛은 일부는 표면에서 바로 반사되고 일부는 굴절되어 표면안으로 들어간다. 이때 반사된 빛은 r의 방향으로 반사된다. 즉 시점이 그 방향에 있지않다면 해당 빛에 영향을 받지않는다는 것이다.(이후 거칠기 개념이 추가되면 정확한 방향에 있지않더라도 일부 빛은 영향을 받을 수 도 있게된다.)
이러한 반영 반사광을 계산하는 것에는 다음 두가지 사항을 사용한다.
프레넬 효과
프레넬 효과는 빛이 표면을 때린 각도와 해당 표면의 재질에 의해 반사,굴절되는 빛의 비율이 결정되는 효과이다. 빛이 해당 표면을 비스듬하게 때릴 수록 반사율은 올라간다.
실제 프레넬 효과 공식은 굉장히 복잡하기에 실시간 렌더링에서 그대로 사용하는 경우는 드물다. 대신 슐릭 근사라는 공식이 자주 쓰인다. 법선벡터와의 각도 a로 표면을 때린 빛이 반사되는 비율은 다음과 같이 구한다.
R(a) = R(0) + (1-R(0))(1-cos(a))5
여기서 R(0)는 수직으로 표면을 때렸을때의 해당 재질에서의 반사율로 재질의 특성값이다. R(a)는 이러한 특성값과 각도로 구할 수 있다. 추가로 R(0) 및 R(a)는 3차원 벡터로 반사율은 각 색상별로 별개로 지정될 수 있다.
표면 거칠기
한 표면점은 미시적 관점에서 미시 표면이다. 그리고 현실의 물체들은 표면이 완전히 매끄럽지 않고 거칠하기에 미시 표면에는 수많은 삐뚤어진 미시법선들이 있다. 이러한 미시법선들이 거시법선에 비해 얼마나 삐뚤어진 비율이 많느냐가 바로 표면 거칠기이다.
빛이 한 방향에서 표면점을 때렸을 때 원래라면 법선에 의해 한방향으로만 광선이 가겠지만 거칠기가 도입되면 미시법선들의 비율에 의해 일정 범위로 법선들이 퍼져나간다. 여기서 우리에게 필요한 정보는 광선에서 반사된 빛이 우리 시점으로 가게하는 미시법선들의 비율, 즉 벡터 h에 해당하는 미시법선들의 비율이다. 그리고 이러한 비율이 곧 반영반사된 빛에서 우리 눈으로 전달되는 세기의 비율이 되게된다. 거칠기는 재질의 특성으로 설정하는 값이기에 거칠기에 따른 미시법선들의 비율식은 n과 h사이의 각도에 따라 비선형적으로 감소되는 공식을 적절히 사용하면 된다. 우리는 다음 공식을 사용한다. n과 h사이의 각도롤 b라고 하자
p(b) = cosm(b) = (n⋅h)m
여기서 m이 높아 질수록 각도에 따라 미시법선의 비율이 더 크게 줄어든다. 즉 여기서 m은 거칠기의 반대 광택도가 된다. 이후 재질의 특성에서 거칠기를 ro라고 할때 (1-ro)*256으로 m을 구해 사용한다.
추가로 거칠기에 따른 미시법선들에서 미시적인 람베르트 코사인 법칙들이 추가적으로 발생한다. 이러한 현상도 공식에 넣으려면 광택도에 따라 반사율을 전체적으로 상승시켜주면 된다. 따라서 미시법선 비율식에 다음의 공식을 p(b) = (m+8/8) x (n⋅h)m
근데 이 식은 1이상의 값이 나와 이후 최종적인 반영 반사율의 값이 1이상이 나올 수 있다. 이는 이후 최종 반영 반사광 계산에서 처리한다.
최종 반영 반사광
최종 반영 반사광은 다음과 같이 구한다.
반영 반사광 = ( max(n⋅L,0) * E ) ⓧ R(h와 n의 각도)*{(m+8/8) x (n⋅h)m}
이때 R(h와 n의 각도){(m+8/8) x (n⋅h)m} 이 부분이 (1,1,1)이상이 될 수 있기에 [0,1] 구간의 빛을 사용하는 우리 방식에 맞춰 S= R(h와 n의 각도){(m+8/8) x (n⋅h)m}라 할때 s/(s+(1,1,1))을 s대신 사용한다. 따라서 최종 반영반사광은 다음과 같다,
최종 반영 반사광 = ( max(n⋅L,0) * E ) ⓧ s/(s+(1,1,1))
주변 반사광
주변 반사광은 임의로 정의하는 주변광 상수로 계산한다. 주변광 상수 벡터를 A라 하자
주변 반사광 = A ⓧ m
최종 반사광
한 광원에 의한 특정 표면점이 시점에서 빛나게 될 빛은 다음과 같다.
최종 반사광 = 주변 반사광 + 분산 반사광 + 반영 반사광
재질
재질의 특성들을 정리하면 다음과 같다.
분산 반사율
프레넬 R(0)
거칠기
코드 구현적으로는 다음 특성들도 가진다.
재질 이름
재질 상수버퍼 인덱스
더티 플레그
추가로 이후 텍스처가 추가되면 다음 특성들도 가지게 된다.
연관된 텍스처 자원(인덱스)
텍스처 변환 행렬
추가로 렌더링 시 재질에 대한 정보를 담는 부분은 대표적으로 다음 두가지가 있다.
상수버퍼로 달기
한 드로우 명령마다 한 재질을 상수버퍼로 설정한다.
정점 특성에 달기
정점 별로 재질 특성을 설정하여 삼각보간을 통해 각 표면점(픽셀)별로 재질 특성이 설정된다.
이후 몇 예제들에서는 상수버퍼로 다는 방식을 채택한다.
평행광
이제 실제 빛을 내는 광원들을 알아보자
평행광은 전역에서 위치에 관계없이 동일한 세기의 동일한 방향으로 발생하는 빛이다. 응용프로그램 내 공간에서의 위치변화가 의미가 없을정도로 굉장히 멀고 강한 광원에서의 빛은 모든 위치에서 동일한 세기와 방향으로 봐도 무방하다. 가장 대표적인 예시가 태양에 의한 빛이다.
이러한 평행광은 빛의 세기와 빛의 방향 두가지로 정의된다.
점광
점광은 한 위치에서 360도 전 방향으로 빛을 내는 광원이다. 대표적으로는 전구가 있다. 점광 광선의 표면 도달방향은 광원에서 표면점 위치로의 벡터가 된다. 빛의 세기는 광원과 표면점 위치의 거리에 따라 세기가 점점 감소하는 공식을 사용한다. 물리적으로 거리와 빛의 세기의 관계는 역제곱 법칙을 따르지만 성능을 위해 start거리 에서 end 거리로 세기가 선형적으로 감소하는 공식을 여기서 사용한다.
0~1 한정((끝거리-d)/(끝거리 - 시작거리))
공식을 사용하면 표면점까지의 거리가 광원에서부터 시작거리까지 사이라면 1의 세기비율을, 시작거리에서 끝 거리 사이라면 1에서 0으로 선형감소하는 시게비율을, 끝거리 이상이라면 0의 세기비율을 가진다.
점광은 광원 위치와 빛의 시작세기, 시작거리, 끝 거리를 가진다.
점적광
점적광은 한 위치에서 원뿔모양으로 빛을 내는 광원이다. 대표적으로는 손전등이 있다. 점적광 광선의 표면 도달방향은 점광과 동일하다. 빛의 세기는 점광의 거리감소 공식을 적용한 후 점적광의 감소를 한번더 적용한다. 점적광의 감소는 세기비율이 광선의 방향이 원뿔 방향과 같을 때 1이며 둘 사이의 각도가 벌이질 수록 0으로 줄어든다. 원뿔 계수를 s라 할때 다음과 같은 공식을 쓸 수있다.
각도 a에서의 비율 = max(cos(a),0)s = max(-L⋅원뿔방향,0)s
각도가 0일때 1에서 90도일때 0으로 감소하는 형태이다. 원뿔 계수가 커질 수록 각도에 따른 감소가 커져 원뿔이 좁아지는 효과가 생긴다. 정확하게는 180도 방향으로 빛을 내는 것이지만 s에 따라 겉부분은 거의 의미없는 수준의 작은 빛만을 내므로 원뿔의 형태가 나타난다.
점적광은 점광의 특성에 더해 원뿔 계수와 방향을 가진다.
빛의 누적
위에서 여러 반사광을 통해 한 광원에서 출발한 광선이 표면점에서 반사되어 시점에 들어오는 빛을 구할 수 있었다. 그런데 한 장면엔 여러개의 광원이 있을 수 있다. 이때 표면점은 최종적으로 각 광원들에 의해 반사된 빛의 누적, 즉 합에 해당하는 색으로 시점에서 보이게 된다. 따라서 장면에서 해당 표면점에 영향을 끼치는 각 광원에 대해 반사광 계산을 수행하고 이들을 모두 합한뒤 [0,1]구간으로 한정하여 해당 픽셀단편의 색상을 결정하면 된다.
참고서적
DirectX 12를 이용한 3D 게임 프로그래밍 입문
'그래픽스 > DirectX12' 카테고리의 다른 글
| [Directx12][9장]텍스처 (0) | 2023.03.21 |
|---|---|
| [Directx12][8장][2]HLSL 구조체 채우기 (0) | 2023.03.21 |
| [Directx12][7장]파이프라이닝2 (0) | 2023.03.21 |
| [Directx12][6장][2]파이프라이닝 구현 (0) | 2023.03.21 |
| [Directx12][6장][1]파이프라이닝 구현 - 기본 지식 (0) | 2023.03.21 |